Answer:
![\sqrt[2]{8}](https://img.qammunity.org/2022/formulas/mathematics/high-school/l4s6lippndf0empisv2663ah31a21557mv.png)
Explanation:
Remember the basic format of a fraction raised to a fractional exponent:
![a^(b)/(c)=\sqrt[b]{a^c}](https://img.qammunity.org/2022/formulas/mathematics/high-school/ivxqzzkay70s9xs14eacw4nqjofclbce3a.png)
Some terms to keep in mind are the following:
(a) is the base
(c) is the exponent
(b) is the index
Apply this information to the given problem:
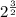
In this case, (2) is the base, and the index; (3) is the exponent. Apply the general format of the fraction exponent to change the expression from an exponent to a radical.
![2^(3)/(2)=\sqrt[2]{2^3}](https://img.qammunity.org/2022/formulas/mathematics/high-school/zjheelajy4xr4zph4xb4k6x1ndfge54e9u.png)
Simplify the term under the radical:
![\sqrt[2]{2^3}=\sqrt[2]{8}](https://img.qammunity.org/2022/formulas/mathematics/high-school/et99yk6jezv3c2zc1hs125jmdm4noa4a7b.png)