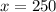Answer:
The length of each side of the city is 250b
Explanation:
Given
 --- tree distance from north gate
--- tree distance from north gate
 --- movement from south gate
--- movement from south gate
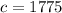 --- movement in west direction from (b)
--- movement in west direction from (b)
See attachment for illustration
Required
Find x
To do this, we have:
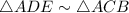 --- similar triangles
--- similar triangles
So, we have the following equivalent ratios

Where:
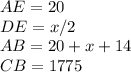
Substitute these in the above equation
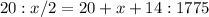
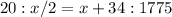
Express as fraction
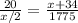

Cross multiply
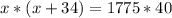
Open bracket
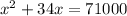
Rewrite as:
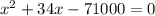
Expand
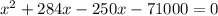
Factorize
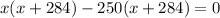
Factor out x + 284
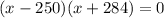
Split
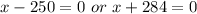
Solve for x

x can't be negative;
So: