Question

An investor has $150,000 to invest in two types of investments. Type A pays 5% annually and type B pays 6% annually. To have a well-balanced portfolio, the investor imposes the following conditions. At least one-third of the total portfolio is to be allocated to type A investments and at least one-third of the portfolio is to be allocated to type B investments. What is the optimal amount that should be invested in each investment

Answer 1

Investment in A $50,000

Investment in B $100,000

Step-by-step explanation:

The total amount available for two investments is $150,000. There are two different investment options available. Type A has 5% annual return and Type B has 6% annual return. The objective equation will be;

0.05A + 0.06B
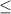`\leq` 5.5%

One third should be allocated to investment A and investment B.

0.33A + 0.33B
`\geq` 0

The risk factor of investments is assumed to be equal then investment B provides more return than investment A.

Investment in A = $150,000 * 0.334 = $50,000

Investment in B = $150,000 * 0.667 = $100,000