Answer:
The sample size must be of 47,059,600.
Explanation:
We have to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
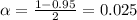
Now, we have to find z in the Z-table as such z has a p-value of
 .
.
That is z with a p-value of
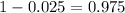 , so Z = 1.96.
, so Z = 1.96.
Now, find the margin of error M as such

In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
Standard deviation:
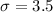
If you want the error bound E of a 95% confidence interval to be less than 0.001, how large must the sample size n be?
This is n for which M = 0.001. So

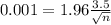
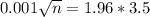
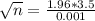
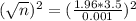

The sample size must be of 47,059,600.