Answer:
0.0022 = 0.22% probability that he randomly plants the trees so that all 6 redwoods are next to each other and all 6 pine trees are next to each other.
Explanation:
The trees are arranged, so the arrangements formula is used to solve this question. Also, a probability is the number of desired outcomes divided by the number of total outcomes.
Arrangements formula:
The number of possible arrangements of n elements is given by:
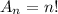
Desired outcomes:
Two cases:
6 redwoods(6! ways) then the 6 pine trees(6! ways)
6 pine trees(6! ways) then the 6 redwoods(6! ways)
So

Total outcomes:
12 trees, so:

What is the probability that he randomly plants the trees so that all 6 redwoods are next to each other and all 6 pine trees are next to each other?

0.0022 = 0.22% probability that he randomly plants the trees so that all 6 redwoods are next to each other and all 6 pine trees are next to each other.