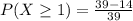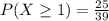Question

Suppose a deck of cards contains 13 cards:

5 green cards numbered 1-5, 4 red cards numbered 1-4, and 4 blue cards numbered 1-4.
For 3.1-3.3, 5 draws are made without replacement. X is the number of green cards drawn and Y is the number of red cards drawn. Z is the sum of the numbers on the tickets.
G1 = first card is green
G2 = second card is green
Enter the probability as a fraction.
P(at least one green) = ______.

Answer 1

`P(G_1) = (5)/(13)`

`P(G_2) = (1)/(3)`

`P(X \ge 1) = (25)/(39)`

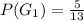
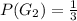
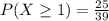
Explanation:

Given

`G = 5`

`R = 4`

`B = 4`

`n = 13`

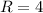
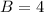
Solving (a):
`P(G_1)`

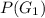
This is calculated as:

`P(G_1) = (G)/(n)`

`P(G_1) = (5)/(13)`

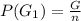
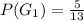
Solving (b):
`P(G_2)`

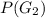
This is calculated as:

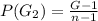`P(G_2) = (G - 1)/(n - 1)` -- this is so because the selection is without replacement

`P(G_2) = (5 - 1)/(13 - 1)`

`P(G_2) = (4)/(12)`

`P(G_2) = (1)/(3)`

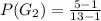
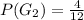
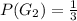
Solving (c):
`P(X \ge 1)`

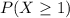
Using the complement rule, we have:

`P(X \ge 1) = 1 - P(X = 0)`

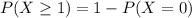
To calculate
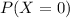`P(X = 0)`, we have:

`G = 5` --- Green

`G' = 8` ---- Not green

The probability that both selections are not green is:

`P(X = 0) = P(G'_1) * P(G'_2)`

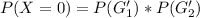
So, we have:

`P(X = 0) = (G')/(n) * (G'-1)/(n-1)`

`P(X = 0) = (8)/(13) * (8-1)/(13-1)`

`P(X = 0) = (8)/(13) * (7)/(12)`

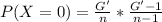
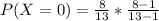
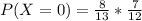
Simplify

`P(X = 0) = (2)/(13) * (7)/(3)`

`P(X = 0) = (14)/(39)`

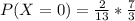
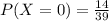
Recall that:

`P(X \ge 1) = 1 - P(X = 0)`

`P(X \ge 1) = 1 - (14)/(39)`

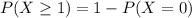
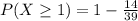
Take LCM

`P(X \ge 1) = (39 -14)/(39)`

`P(X \ge 1) = (25)/(39)`