Answer:
0.9378 = 93.78% probability that a randomly selected person has diabetes, given that his test is positive.
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is
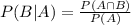
In which
P(B|A) is the probability of event B happening, given that A happened.
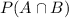 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Positive test
Event B: Person has diabetes.
Probability of a positive test:
0.95 out of 0.1(person has diabetes).
0.007 out of 1 - 0.1 = 0.9(person does not has diabetes). So
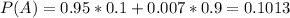
Probability of a positive test and having diabetes:
0.95 out of 0.1. So
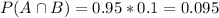
What is the probability that a randomly selected person has diabetes, given that his test is positive?
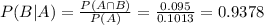
0.9378 = 93.78% probability that a randomly selected person has diabetes, given that his test is positive.