Question

cho tứ giác ABCD. Gọi M,N,P,Q là trung điểm của các cạnh AB, CD, AD, BC. Chứng minh rằng vecto MP = vecto QN, vecto MQ = vecto PN

Answer 1

Explanation:

Xét tam giác DAB có: P là trung điểm AD, M là trung điểm AB

=> MP là đường trung bình của tam giác DAB => MP//BD và MP=
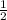`(1)/(2)`BD (1)

Xét tam giác DBC có: N là trung điểm DC, Q là trung điểm BC

=> QN là đường trung bình của tam giác DBC => QN//BD và QN=
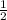`(1)/(2)`BD (2)

Từ (1) và (2) => vecto MP song song cùng chiều với vecto QN

và độ dài MP = độ dài QN =
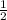`(1)/(2)`BD

=> vecto MP = vecto QN

Tương tự xét các tam giác DAC và tam giác ABC => vecto MQ = vecto PN