Question

A large wooden box, as shown, has a volume of 4352 ft3. The box is a right square prism with a base with sides that each measure 16 ft. What is h, the height of the box?

Answer 1

17

Explanation:

Answer 2

Volume of a Prism

To find the volume of a prism, we can use the following formula:

`V=base\hspace{3}area*height`

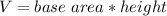
Although this formula is typically used to find the volume of a prism, we can also use it to find the base area or height, as long as we re-arrange it accordingly.

For a rectangular prism, the base area is solved using the following formula:

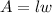`A=lw` ⇒ where l is the length and w is the width

Solving the Question

We're given:

• V = 4352 ft³
• l = 16 ft
• w = 16 ft
• We need to solve for the height of the box.

First, find the base area:

`A=lw\\A=16^2\\A=256`

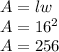
Therefore, the base area is equal to 256 ft².

Now, modify the volume formula to isolate the height:

`V=base\hspace{3}area*height`

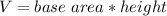
⇒ Divide both sides by the base area:

`\frac{V}{base\hspace{3}area}=\frac{base\hspace{3}area*height}{base\hspace{3}area}\\\\\frac{V}{base\hspace{3}area}=height\\\\height=\frac{V}{base\hspace{3}area}`

⇒ Plug in the given values:

`height=(4352)/(256)\\\\height=17`

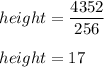
Therefore, the height of the box is 17 ft.

Answer

The height of the box is 17 ft.