Question

Find the number of terms, n, in the arithmetic series whose first term is 13, the common difference is 7, and the sum is 2613.

A26
B27
C23
D32

Answer 1

A

Explanation:

Recall that the sum of an arithmetic series is given by:

`\displaystyle S = (n)/(2)\left(a + x_n\right)`

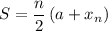
Where n is the number of terms, a is the first term, and x_n is the last term.

We know that the initial term a is 13, the common difference is 7, and the total sum is 2613. Since we want to find the number of terms, we want to find n.

First, find the last term. Recall that the direct formula for an arithmetic sequence is given by:

`x_n=a+d(n-1)`

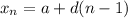
Since the initial term is 13 and the common difference is 7:

`x_n=13+7(n-1)`

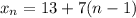
Substitute:

`\displaystyle S = (n)/(2)\left(a + (13+7(n-1)\right)`

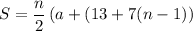
We are given that the initial term is 13 and the sum is 2613. Substitute:

`\displaystyle (2613)=(n)/(2)((13)+(13+7(n-1)))`

Solve for n. Multiply both sides by two and combine like terms:

`5226 = n(26+7(n-1))`

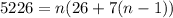
Distribute:

`5226 = n (26+7n-7)`

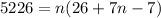
Simplify:

`5226 = 7n^2+19n`

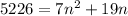
Isolate the equation:

`7n^2+19n-5226=0`

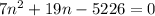
We can use the quadratic formula:

`\displaystyle x = (-b\pm√(b^2-4ac))/(2a)`

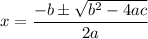
In this case, a = 7, b = 19, and c = -5226. Substitute:

`\displaystyle x =(-(19)\pm√((19)^2-4(7)(-5226)))/(2(7))`

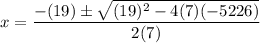
Evaluate:

`\displaystyle x = (-19\pm√(146689))/(14) = (-19\pm 383)/(14)`

Evaluate for each case:

`\displaystyle x _ 1 = (-19+383)/(14) = 26\text{ or } x _ 2 = (-19-383)/(14)=-(201)/(7)`

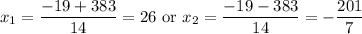
We can ignore the second solution since it is negative and non-natural.

Therefore, there are 26 terms in the arithmetic series.

Our answer is A.