Answer:
The range of weights of the middle 99.7% of M&M’s is between 0.8187 and 1.0203.
Explanation:
The Empirical Rule states that, for a normally distributed random variable:
Approximately 68% of the measures are within 1 standard deviation of the mean.
Approximately 95% of the measures are within 2 standard deviations of the mean.
Approximately 99.7% of the measures are within 3 standard deviations of the mean.
Sample mean:
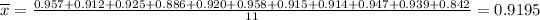
Sample standard deviation:

What is the range of weights of the middle 99.7% of M&M’s?
By the Empirical Rule, within 3 standard deviations of the mean, so:
0.9195 - 3*0.0336 = 0.8187.
0.9195 + 3*0.0336 = 1.0203.
The range of weights of the middle 99.7% of M&M’s is between 0.8187 and 1.0203.