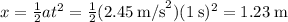Question

Two masses of 3 kg and 5 kg are connected by a light string that passes over a smooth polley as shown in the Figure.

QL
Determine:
i. the tension in the string,
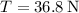
ii. the acceleration of each mass, and
iii. the distance each mass moves in the first second of motion if they start from rest​

Answer 1

i.
`T = 36.8\:\text{N}`

ii.
`a = 2.45\:\text{m/s}^2`

iii.
`x = 1.23\:\text{m}`

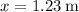
Step-by-step explanation:

Let's write Newton's 2nd law for each object. We will use the sign convention assigned for each as indicated in the figure. Let T be the tension on the string and assume that the string is inextensible so that the two tensions on the strings are equal. Also, let a be the acceleration of the two masses. And
`m_1 = 3\:\text{kg}` and
`m_2 = 5\:\text{kg}`

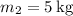
Forces acting on m1:

`T - m_1g = m_1a\:\:\:\:\:\:\:(1)`

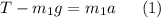
Forces acting on m2:

`m_2g - T = m_2a\:\:\:\:\:\:\:(2)`

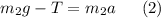
Combining Eqn(1) and Eqn(2) together, the tensions will cancel out, giving us

`m_2g - m_1g = m_2a + m_1a`

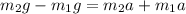
or

`(m_2 - m_1)g = (m2 + m_1)a`

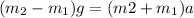
Solving for a,

`a = \left((m_2 - m_1)/(m_2 + m_1)\right)g`

`\:\:\:\:= \left(\frac{5\:\text{kg} - 3\:\text{kg}}{5\:\text{kg} + 3\:\text{kg}}\right)(9.8\:\text{m/s}^2)`

`\:\:\:\:= 2.45\:\text{m/s}^2`

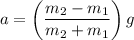
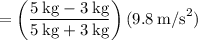
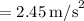
We can solve for the tension by using this value of acceleration on either Eqn(1) or Eqn(2). Let's use Eqn(1).

`T - (3\:\text{kg})(9.8\:\text{m/s}^2) = (3\:\text{kg})(2.45\:\text{m/s}^2)`

`T = (3\:\text{kg})(9.8\:\text{m/s}^2) + (3\:\text{kg})(2.45\:\text{m/s}^2)`

`\:\:\:\:= 29.4\:\text{m/s}^2 + 7.35\:\text{m/s}^2 = 36.8\:\text{N}`

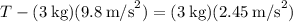
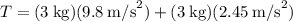
Assuming that the two objects start from rest, the distance that they travel after one second is given by

`x = (1)/(2)at^2 = (1)/(2)(2.45\:\text{m/s}^2)(1\:\text{s})^2 = 1.23\:\text{m}`