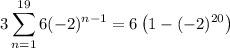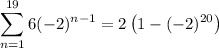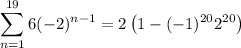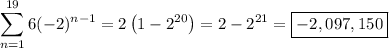(1) This series consists of terms of an arithmetic sequence:
179 - 173 = 6
173 - 167 = 6
and so on, so that the n-th term in the series is (for n ≥ 1)
a(n) = 179 - 6 (n - 1) = 185 - 6n
Then the sum of the first 53 terms is
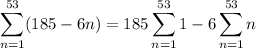
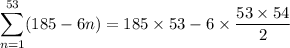
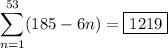
(2) This series has terms from a geometric sequence:
-12 / 6 = -2
24/(-12) = -2
-48/24 = -2
and so on. The n-th term is (again, for n ≥ 1)
a(n) = 6 (-2)ⁿ⁻¹
and the sum of the first 19 terms is
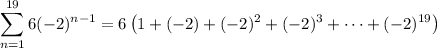
Multiply both sides by -2 :
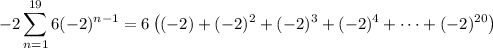
Subtracting this from the first sum gives
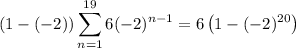
and solving for the sum, you get