Given:
If you divide any natural number n by 4, you get a remainder r.
To find:
The values of r if
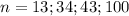 . Also find the domain and range.
. Also find the domain and range.
Solution:
It is given that any natural number n by 4, you get a remainder r.
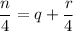
Where, n is a natural number, q is quotient, r is the remainder.
For
 ,
,
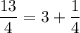
So,
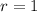 .
.
For
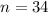 ,
,
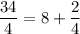
So,
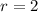 .
.
For
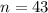 ,
,

So,
 .
.
For
 ,
,
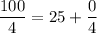
So,
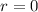 .
.
Therefore, the required value are
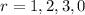 if
if
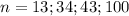 respectively.
respectively.
The domain of the function is
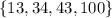 and the range of the function is
and the range of the function is
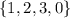 .
.