Answer:
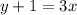
OR
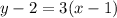
Explanation:
Hi there!
Point-slope form:
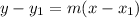 where m is the slope and
where m is the slope and
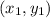 is a point
is a point
1) Determine the slope (m)
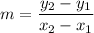 where two points that fall on the line are
where two points that fall on the line are
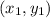 and
and
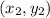
Plug in the points (0,-1) and (1,2):
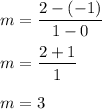
Therefore, the slope of the line is 3. Plug this into
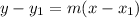 :
:
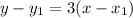
2) Plug a point into the equation
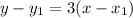
Because we're given two points, there are two ways we can write the equation:
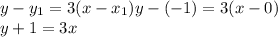
OR
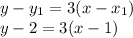
I hope this helps!