Question

NO LINKS OR ANSWERING QUESTIONS YOU DON'T KNOW. THIS IS NOT A TEST OR AN ASSESSMENT!! Please help me with these math problems. Chapter 12 part 2 PLEASE SHOW WORK!!!

4a. a_n = 2(1/3 + a_n-1), a_1 = 4

4b. a_n= n/(a_n-1), a_1 = 6

4c. 1/6, 2/3, 8/3, . . .

Answer 1

Problem 4a

The instructions are incomplete. You set up the recursive formula, but didn't ask any question about said formula.

I'll assume that your teacher wants you to list out a few terms. I'll list out the first five terms.

The notation a_1 = 4 is the same as writing
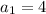`a_1 = 4` where the '1' is a subscript. It tells us that the first term is 4.

The nth term a_n or
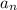`a_n` is defined as such

`a_n = 2*(1/3 + a_(n-1))\\\\`

Notice how if we replaced n with 2, then we get

`a_n = 2*(1/3 + a_(n-1))\\\\a_2 = 2*(1/3 + a_(2-1))\\\\a_2 = 2*(1/3 + a_1)\\\\`

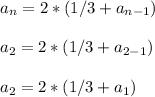
So the second term is directly tied to the first term, or it is dependent on it.

We'll replace a_1 with 4 to get the following

`a_2 = 2*(1/3 + a_1)\\\\a_2 = 2*(1/3 + 4)\\\\a_2 = 2*(1/3 + 12/3)\\\\a_2 = 2*(13/3)\\\\a_2 = 26/3\\\\`

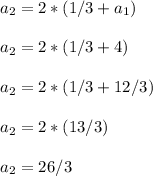
So the second term is 26/3.

As you can guess, the third term is going to be found in a similar fashion

`a_n = 2*(1/3 + a_(n-1))\\\\a_3 = 2*(1/3 + a_(3-1))\\\\a_3 = 2*(1/3 + a_2)\\\\a_3 = 2*(1/3 + 26/3)\\\\a_3 = 2*(27/3)\\\\a_3 = 2*(9)\\\\a_3 = 18\\\\`

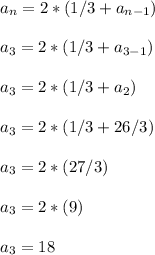
So 18 is the third term.

We'll repeat for n = 4 to get the fourth term.

`a_n = 2*(1/3 + a_(n-1))\\\\a_4 = 2*(1/3 + a_(4-1))\\\\a_4 = 2*(1/3 + a_3)\\\\a_4 = 2*(1/3 + 18)\\\\a_4 = 2*(1/3 + 54/3)\\\\a_4 = 2*(55/3)\\\\a_4 = 110/3\\\\`

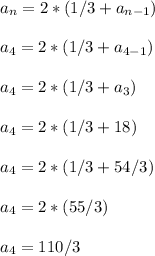
The fourth term is 110/3.

Lastly, we'll plug in n = 5

`a_n = 2*(1/3 + a_(n-1))\\\\a_5 = 2*(1/3 + a_(5-1))\\\\a_5 = 2*(1/3 + a_4)\\\\a_5 = 2*(1/3 + 110/3)\\\\a_5 = 2*(111/3)\\\\a_5 = 2*(37)\\\\a_5 = 74\\\\`

The fifth term is 74.

Answer: The first five terms are 4, 26/3, 18, 110/3, 74

==============================================================

Problem 4b

Again, the instructions are missing. I'll assume the same thing as problem 4a.

`a_1 = 6` is the first term

Plug n = 2 into the first equation to get

`a_n = (n)/(a_(n-1))\\\\a_2 = (2)/(a_(2-1))\\\\a_2 = (2)/(a_(1))\\\\a_2 = (2)/(6)\\\\a_2 = (1)/(3)\\\\`

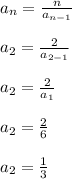
The second term is 1/3.

Repeat for n = 3

`a_n = (n)/(a_(n-1))\\\\a_3 = (3)/(a_(3-1))\\\\a_3 = (3)/(a_(2))\\\\a_3 = (3)/(1/3)\\\\a_3 = 3/(1)/(3)\\\\a_3 = 3*(3)/(1)\\\\a_3 = 9\\\\`

The third term is 9

Repeat for n = 4.

`a_n = (n)/(a_(n-1))\\\\a_4 = (4)/(a_(4-1))\\\\a_4 = (4)/(a_(3))\\\\a_4 = (4)/(9)\\\\`

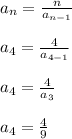
The fourth term is 4/9

Repeat for n = 5

`a_n = (n)/(a_(n-1))\\\\a_5 = (5)/(a_(5-1))\\\\a_5 = (5)/(a_(4))\\\\a_5 = 5 / a_(4)\\\\a_5 = 5 / (4)/(9)\\\\a_5 = 5 * (9)/(4)\\\\a_5 = (5)/(1) * (9)/(4)\\\\a_5 = (5*9)/(1*4)\\\\a_5 = (45)/(4)\\\\`

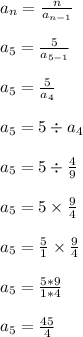
Answer: The first five terms are 6, 1/3, 9, 4/9, 45/4

==============================================================

Problem 4c

I'm not much help here for this problem. Not only are the instructions missing, but it's not clear how this sequence is set up. If I had to guess, it's somehow recursively defined. How exactly, I'm not sure. I would ask your teacher for any clarification.