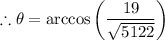Answer:
See below
Explanation:
3. What are two ways that a vector can be represented?
Considering a vector
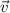 in some vector space
in some vector space
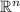 we have
we have
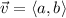
This is the component form. I don't like that way. It is probably used in high school, but
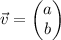
is preferable because the inner product on
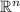 is defined to be
is defined to be
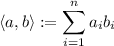
You can also write it using linear form such as
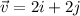
4.
For this question, I think you meant
vectors


Once

Considering that the dot product is
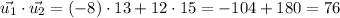
and the norm of
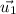 is
is
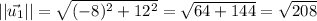
and the norm of
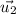 is
is
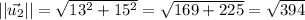
Thus,