Question

Garden Variety Flower Shop uses 500 clay pots a month. The pots are purchased at $3 each. Annual holding costs per pot are estimated to be 25 percent of a pot's purchase price, and ordering costs are $25 per order. The manager has been using an order size of 1,500 flower pots.

a. What additional annual cost is the shop incurring by staying with this order size?
b. Other than cost savings, what benefit would using the optimal order quantity yield (relative to the order size of 1,500)?

Answer 1

The data for the Garden Variety Flower shop is :

Monthly demand, d = 500 clay pots

Annual demand, D = 500 x 12

= 6000 clays

Price, p = $ 3.00 each

Annual carrying cost, h = 25% of price

`$=(25)/(100) * 3$`

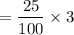
= $0.75

Ordering cost, S = $ 25 per order

a). The optimal order quantity, EOQ

`$EOQ=\sqrt{(2DS)/(h)}$`

`$=\sqrt{(2* 6000 * 25)/(0.75)}$`

`$=\sqrt{(300000)/(0.75)}$`

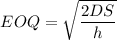
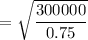
= 632.45

≈ 633

So, the optimal order quantity is 633 clay pots.

Therefore, the annual cost for optimal order quantity 633 clay pots,

`$\text{Total annual cost}_1=\left((D)/(Q) * S \right) + \left((D)/(2) * h \right)$`
`$\text{Total annual cost}_1=\left((6000)/(633) * 25 \right) + \left((633)/(2) * 0.75 \right)$`

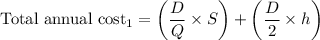
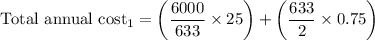
= 236.96 + 237.37

= 474.33

Now calculating the total annual cost for the optimal order quantity 1500 flower pots, as shown below:

`$\text{Total annual cost}_2=\left((D)/(Q) * S \right) + \left((D)/(2) * h \right)$`

`$\text{Total annual cost}_2=\left((6000)/(1500) * 25 \right) + \left((1500)/(2) * 0.75 \right)$`

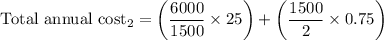
= 100 + 562.5

= 662.5

Calculating the additional annual cost of the shipping is incurring by staying with the order size, i.e. 1500 flower pots as given below:

Extra cost =
`$\text{total annual cost}_2 - \text{total annual cost}_1 $`

= 662.5 - 474.3

= 188.2

So, the
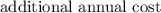`\text{additional annual cost}` is the shop
`\text{incurring}` by staying with this order size is 188.2

b). Calculating the average inventory level of the
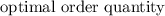`\text{optimal order quantity}` 1500 flowers plots :

Average inventory = Q/2

`$=(1500)/(2)$`

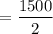
= 750

Calculating the average percentage of the storage space :

`$\text{Percentage of storage space} = \frac{\text{Extra cost}}{\text{average inventory}}* 100$`

`$=(188.2)/(750) * 100$`

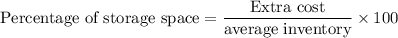
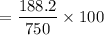
= 0.250 x 100

= 25 %

So, the benefit would be using the
`\text{optimal order quantity}` yield, i.e. 1500 flower plots is 25%.