Solution :
The data is normally distributed.
The standard deviation is 18 days
Here the data is normally distributed and 54 days is 3 days of standard deviation.
Therefore, the percentage of the births that would be
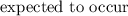 within the 54 days of the mean
within the 54 days of the mean
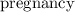 length is given by :
length is given by :
= P( -3 < Z < 3)
= 0.9544
= 95 %
Therefore, about 95% of the births would be
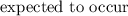 within 54 days of the men
within 54 days of the men
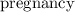 length.
length.