Answer:
C.
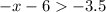
Explanation:
One is asked to find which inequality has (
 ) in its solution set. Remember that an inequality is another way to represent a set of solutions. In essence, it states that all numbers less than; less than or equal to; greater than; or greater than or equal to, are a part of the solution. One simplifies an inequality in a similar manner to how one simplifies an equation, by using inverse operations and simplification. Just note that when multiplying or dividing the inequality by a negative number, one has to flip the inequality sign to ensure the expression remains true.
) in its solution set. Remember that an inequality is another way to represent a set of solutions. In essence, it states that all numbers less than; less than or equal to; greater than; or greater than or equal to, are a part of the solution. One simplifies an inequality in a similar manner to how one simplifies an equation, by using inverse operations and simplification. Just note that when multiplying or dividing the inequality by a negative number, one has to flip the inequality sign to ensure the expression remains true.
Simplify each of the inequalities, then evaluate to see which one has (
 ) as a part of its solution set.
) as a part of its solution set.
A.
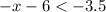


B.

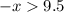

C.
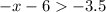
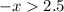

D.
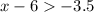
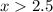
As can be seen, option (C
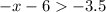 ) is the only one that fits this requirement. Since option (C) simplifies down to (
) is the only one that fits this requirement. Since option (C) simplifies down to (
 ) or in words, (x) is less than (-2.5). This option is the only one that fits the solution since (-3) is less than (-2.5).
) or in words, (x) is less than (-2.5). This option is the only one that fits the solution since (-3) is less than (-2.5).