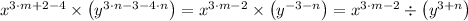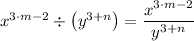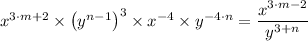Answer:
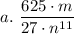
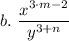
Explanation:
The question relates with rules of indices
(a) The give expression is presented as follows;
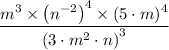
By expanding the expression, we get;
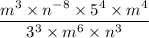
Collecting like terms gives;
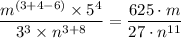
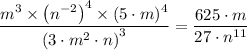
(b) The given expression is presented as follows;
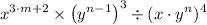
Therefore, we get;
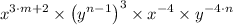
Collecting like terms gives;