Answer:
1.24
Step-by-step explanation:
The resistivity of copper
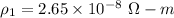
The resistivity of Aluminum,
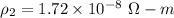
The wires have same resistance per unit length.
The resistance of a wire is given by :
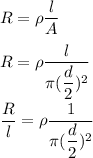
According to given condition,
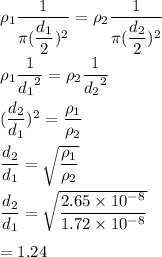
So, the required ratio of the diameter of Aluminum to Copper wire is 1.24.