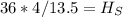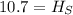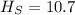Answer:
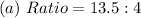
(b) The height of the smaller bucket is 10.7
Explanation:
Given
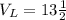
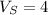
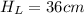
Solving (a): The ratios
This is represented as:
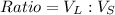
So, we have:
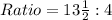
Express as decimal
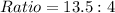
Solving (b): The height of the smaller bucket
The ratio of the heights is:
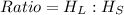
So, we have:
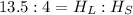
Substitute known value
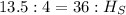
Express as fraction
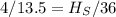
Multiply by 36