Answer:
The endpoints of the latus rectum are
 and
and
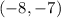 .
.
Explanation:
A parabola with vertex at point
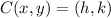 and whose axis of symmetry is parallel to the y-axis is defined by the following formula:
and whose axis of symmetry is parallel to the y-axis is defined by the following formula:
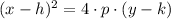 (1)
(1)
Where:
 - Independent variable.
- Independent variable.
 - Dependent variable.
- Dependent variable.
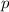 - Distance from vertex to the focus.
- Distance from vertex to the focus.
 ,
,
 - Coordinates of the vertex.
- Coordinates of the vertex.
The coordinates of the focus are represented by:
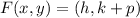 (2)
(2)
The latus rectum is a line segment parallel to the x-axis which contains the focus. If we know that
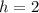 ,
,
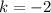 and
and
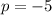 , then the latus rectum is between the following endpoints:
, then the latus rectum is between the following endpoints:
By (2):
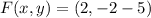
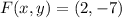
By (1):
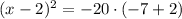
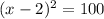
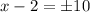
There are two solutions:
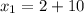
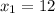
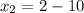

Hence, the endpoints of the latus rectum are
 and
and
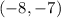 .
.