Question

The moon Phobos orbits Mars

(mass = 6.42 x 1023 kg) at
a distance
of 9.38 x 106 m. What is its period of
orbit?
[?]s

Answer 1

Step-by-step explanation:

We are basically needing to solve for the time in the equation d = rt, where d is the distance around Mars (aka the circumference), r is the velocity, and t is time. We need to find the circumference and the velocity. We will begin with the velocity.

Because the gravitational attraction between Phobos and Mars provides the centripetal acceleration necessary to keep Phobos in its (sort of) circular path, the equation we use for this is:

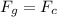`F_g=F_c` which says that Force supplied by gravity is equal to the centripetal force. Expanding that:

`(Gm_(Phobos)m_(Mars))/(r^2)=(m_(Phobos)v^2)/(r)`

When we move that around mathematically to solve for the velocity value, what we end up with is:

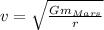`v=\sqrt{(Gm_(Mars))/(r)` and filling in:

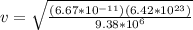`v=\sqrt{((6.67*10^(-11))(6.42*10^(23)))/(9.38*10^6) }` and we get that

v = 2100 m/s

Now for the circumference:

C = 2πr and

C = 2(3.1415)(9.38 × 10⁶) so

C = 5.9 × 10⁷

Putting that all together in the C = vT equation:

5.9 × 10⁷ = 2100T so

T = 2.8 × 10⁴ sec or 7.8 hours