Given:
The given geometric sequence is:
0.0625, 0.25, 1, ..., 4194304
To find:
The number of terms in the given geometric sequence.
Solution:
We have,
0.0625, 0.25, 1, ..., 4194304
Here, the first term is 0.0625 and the common ratio is:
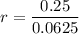
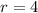
The nth term of a geometric sequence is:
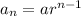
Where, a is the first term and r is the common ratio.
Putting
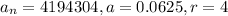 in the above formula, we get
in the above formula, we get
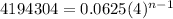
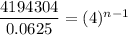
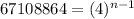
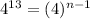
On comparing both sides, we get
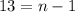
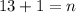
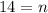
Therefore, the number of terms in the given geometric sequence is 14.