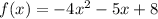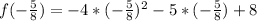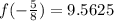Question

Select the correct answer.

Which is the minimum or maximum value of the given function?
dndnsn

Answer 1

See explanation

Explanation:

The question is incomplete, as the function is not given. So, I will make an assumption.

A quadratic function is represented as:

`f(x) = ax^2 + bx + c`

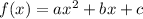
If
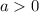`a > 0`, then the function has a minimum x value

E.g.
`f(x) = 4x^2 - 5x + 8` ------
`4 > 0`

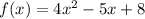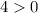
Else, then the function has a maximum x value

E.g.
`f(x)= -4x^2 -5x + 8` ----
`-4 < 0`

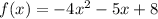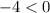
The maximum or minimum x value is calculated using:

`x = -(b)/(2a)`

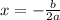
For instance, the maximum of
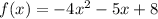`f(x)= -4x^2 -5x + 8` is:

`x = -(-5)/(2*-4)`

`x = -(5)/(8)`

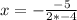
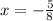
So, the maximum of the function is:

`f(x)= -4x^2 -5x + 8`

`f(-(5)/(8)) = -4 * (-(5)/(8))^2 - 5 *(-(5)/(8)) +8`

`f(-(5)/(8)) = 9.5625`