Given:
The slope of a line is
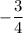 .
.
To find:
The lines in the options are parallel, perpendicular or neither parallel nor perpendicular to the given line.
Solution:
We know that the slopes of parallel lines are equal.
The slope of line Q and the slope of given line are same, i.e.,
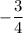 . So, the line Q is parallel to the given line.
. So, the line Q is parallel to the given line.
The slope of a perpendicular line is the opposite reciprocal of the slope of the line because the product of slopes of two perpendicular lines is -1.
The slope of a line is
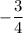 . It means the slope of the perpendicular line must be
. It means the slope of the perpendicular line must be
 . So, the line N is perpendicular to the given line.
. So, the line N is perpendicular to the given line.
The slopes of line M and P are neither equal to the slope of the given line nor opposite reciprocal of the slope of the line.
Therefore, the lines M and P are neither parallel nor perpendicular.