Question

Find a solution to the initial value problem,
y″+12x=0, y(0)=2,y′(0)=−1.

Answer 1

y = -2*x^3 - x + 2

Explanation:

We want to solve the differential equation:

y'' + 12*x = 0

such that:

y(0) = 2

y'(0) = -1

We can rewrite our equation to:

y'' = -12x

if we integrate at both sides, we get:

`\int {y''} \, dx = y'= \int {-12x} \, dx`

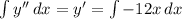
Solving that integral we can find the value of y', so we will get:

y' = -12* (1/2)*x^2 + C = -6*x^2 + C

where C is the constant of integration.

Evaluating y' in x = 0 we get:

y'(0) = -6*0^2 + C = C

and for the initial value problem, we know that:

y'(0) = -1

then:

y'(0) = -1 = C

C = -1

So we have the equation:

y' = -6*x^2 - 1

Now we can integrate again, to get:

y = -6*(1/3)*x^3 - 1*x + K

y = -2*x^3 - x + K

Where K is the constant of integration.

Evaluating or function in x = 0 we get:

y(0) = -2*0^3 - 0 + K

y(0) = K

And by the initial value, we know that: y(0) = 2

Then:

y(0) = 2 = K

K = 2

The function is:

y = -2*x^3 - x + 2