Answer:
3x-4y=3
Explanation:
Hi there!
We are given the equation y-3=
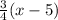 , and we want to write it in standard form
, and we want to write it in standard form
Standard form is given as ax+by=c, where a, b, and c are integer coefficients, a CANNOT be 0 and CANNOT be negative, and b also CANNOT be 0
So let's expand the parentheses in the equation
Do the distributive property
y-3=
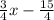
Add 3 to both sides
y=
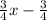
We expanded the parentheses, but the equation is now in slope-intercept form (y=mx+b, where m is the slope and b is the y intercept)
Remember that we want it in standard form, which is ax+by=c
Subtract
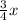 from both sides
from both sides
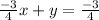
Remember that the coefficients of a, b, and c need to be integers, and also that a (the coefficient in front of x) CANNOT be negative
So multiply both sides by -4
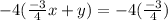
Distribute -4 to every number
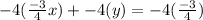
Multiply
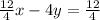
Simplify
3x-4y=3
There's the equation in standard form
Hope this helps!