Question

The pair of figures to the right are similar. The area of one figure is given. Find the area of the other figure to the nearest whole number. Area of larger triangle = 165 ft^2 Thank you!!​

Answer 1

Area of the smaller triangle = 73 square feet

Explanation:

Area of the larger triangle = 165 square feet

Area of a triangle =
`(1)/(2)(\text{Base})(\text{Height})`

`(1)/(2)(\text{Base})(\text{Height})=165`

`(1)/(2)(15)(\text{Height})=165`

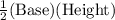
Height = 22 ft

Since, both the triangles are similar.

By the property of similar triangles,

Corresponding sides of the similar triangles are proportional.

Let the height of smaller triangle = h ft

Therefore,
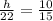
`(h)/(22)=(10)/(15)`

h =
`(22* 10)/(15)`

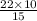
h = 14.67 ft

Area of the smaller triangle =
`(1)/(2)(10)(14.67)`

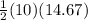
= 73.33

≈ 73 square feet

Answer 2

9514 1404 393

Answer:

73 ft²

Explanation:

The ratio of areas is the square of the ratio of linear dimensions.

smaller area = larger area × ((10 ft)/(15 ft))² = 165 ft² × (4/9)

smaller area = 73 1/3 ft² ≈ 73 ft²