Answer:
Explanation:
To answer this we need only know that negative parabolas are upside down, so by definition, it has a max point at the vertex. To find the vertex (h, k), the easy way to do this is to fill in the following expressions for h and k and solve:
 and
and
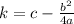 (These are derived from the quadratic formula). Filling in knowing our a = -1, b = -7, c = 12:
(These are derived from the quadratic formula). Filling in knowing our a = -1, b = -7, c = 12:
 and
and
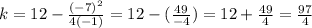 so the vertex (aka max height occurs at
so the vertex (aka max height occurs at
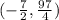 . Depending upon what is meant by stating the max value, we may only need to state the k value (which is the same as the y coordinate, which is an up or down thing as opposed to the x value which is a side to side thing). The domain is all real numbers, as is the case for all x-squared parabolas, and the range is
. Depending upon what is meant by stating the max value, we may only need to state the k value (which is the same as the y coordinate, which is an up or down thing as opposed to the x value which is a side to side thing). The domain is all real numbers, as is the case for all x-squared parabolas, and the range is
R = y ≤ 97/4
I can't see your choices so match them up from these answers to the ones in the list of choices.