Question

The Online Exam from Applied Statistics consists of 6 questions. Statistics show that there is a 75% chance that the student will answer to any one of Exam problems correctly. If the number of attempts for each question is unlimited, find the following probabilities

a. The student will correctly answer the first question after the 4th attempt.
b. The student will correctly answer three questions after 10 total attempts.
c. What is the average number and SD of attempts up to when the student answers all the questions correctly?

Answer 1

a). The probability that the student will
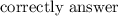`\text{correctly answer}` the 1st question after the 4th attempt.

P (correct in the 4th attempt)

=
`$(1-0.75)^3 * 0.75$`

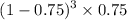
= 0.01171875

b). The probability that the student will
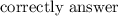`\text{correctly answer}` 3 questions after 10 total attempts.

P( X = 3) for X = B in (n = 10, p = 0.75)

=
`$C(10,30) * 0.75^3 * 0.25^7$`

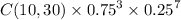
= 0.0031

c). The mean and the standard deviation for the number of attempts up to when the students gets all the questions correct is :

There are = 6 success, p = 0.75.

Therefore, this is a case of a negative binomial distribution.

`$E(X)=(k)/(p)$`

`$=(6)/(0.75)$`

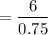
= 8

So,
`$\sigma = (√(k(1-p)))/(p)$`

`$\sigma = (√(6(1-0.75)))/(0.75)$`

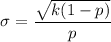
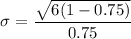
= 1.6330