Question

The function f(x) = - (x + 5) * (x + 1) shown What is the range of the function ? 10 all real numbers loss than or equal to all roal numbers less than or equal to -3 all real numbers groater or equal to 4 numbors greater than or equal to -6

Answer 1

Given:

The function is:

`f(x)=-(x+5)(x+1)`

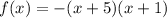
To find:

The range of the function.

Solution:

We have,

`f(x)=-(x+5)(x+1)`

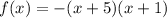
It can be written as:

`f(x)=-(x^2+x+5x+5)`

`f(x)=-(x^2+6x+5)`

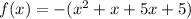
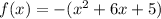
Add and subtract square of half of coefficient of x, i.e.,
`\left((6)/(2)\right)^2=9`.

`f(x)=-(x^2+6x+9-9+5)`

`f(x)=-(x^2+2(x)(3)+3^2-4)`

`f(x)=-(x^2+2(x)(3)+3^2)+4`

`f(x)=-(x+3)^2+4`

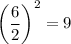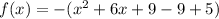
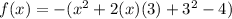
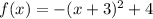
On comparing this equation with
`f(x)=a(x-h)^2+k`, we get

`a=-1`, it means the graph of the function is a downward parabola and the vertex is the point of maxima.

`h=-3`

`k=4`

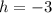
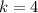
The vertex of the function is (-3,4). So, the value of the function cannot be greater than 4.

Therefore, the range of the function is all real numbers less than or equal to 4.

Note: All options are incorrect.