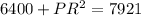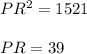Answer:
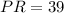
Explanation:
The triangle (PQR) is a right triangle. This means the triangle has a (90) degree angle, such is indicated by the box around one of the angles in the triangle. One of the properties of the sides of a right triangle is the Pythagorean theorem. The Pythagorean theorem states the following:
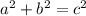
Where (a) and (b) are the legs of the right triangle, or the sides adjacent to the right angle. (c) is the side opposite the right angle of the triangle triangle, in other words, the hypotenuse. Substitute the respective legs into the formula for the Pythagorean theorem and solve for the unknown,
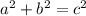
Substitute,
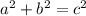
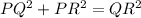
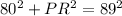
Simplify,
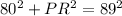
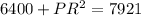
Inverse operations,