Answer:
The concentration of cyclobutane after 875 seconds is approximately 0.000961 M
Step-by-step explanation:
The initial concentration of cyclobutane, C₄H₈, [A₀] = 0.00150 M
The final concentration of cyclobutane, [
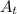 ] = 0.00119 M
] = 0.00119 M
The time for the reaction, t = 455 seconds
Therefore, the Rate Law for the first order reaction is presented as follows;
![\text{ ln} \frac {[A_t]}{[A_0]} = \text {-k} \cdot t }](https://img.qammunity.org/2022/formulas/chemistry/high-school/dzqh92o6unhmziwpis3h7zb4uejzpebmez.png)
Therefore, we get;
![k = \frac{\text{ ln} \frac {[A_t]}{[A_0]}} {-t }](https://img.qammunity.org/2022/formulas/chemistry/high-school/8gwp4ni3tfwxbe6zxdrgi2bjvkk97xpyvz.png)
Which gives;
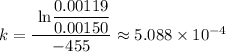
k ≈ 5.088 × 10⁻⁴ s⁻¹
The concentration after 875 seconds is given as follows;
[
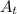 ] = [A₀]·
] = [A₀]·
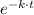
Therefore;
[
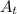 ] = 0.00150 ×
] = 0.00150 ×
 = 0.000961
= 0.000961
The concentration of cyclobutane after 875 seconds, [
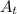 ] ≈ 0.000961 M
] ≈ 0.000961 M