Answer:
Proof in explanataion
Step-by-step explanation:
The basic dimensions are as follows:
MASS = M
LENGTH = L
TIME = T
i)
Given equation is:

where,
H = height (meters)
u = speed (m/s)
g = acceleration due to gravity (m/s²)
Sin Ф = constant (no unit)
So there dimensions will be:
H = [L]
u = [LT⁻¹]
g = [LT⁻²]
Sin Ф = no dimension
Therefore,
![[L] = ([LT^(-1)]^2)/([LT^(-2)])\\\\\ [L] = [L^((2-1))T^((-2+2))]](https://img.qammunity.org/2022/formulas/physics/college/l215dt1qbctth4uxiyjke394soyfa80vt7.png)
[L] = [L]
Hence, the equation is proven to be homogenous.
ii)
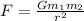
where,
F = Force = Newton = kg.m/s² = [MLT⁻²]
G = Gravitational Constant = N.m²/kg² = (kg.m/s²)m²/kg² = m³/kg.s²
G = [M⁻¹L³T⁻²]
m₁ = m₂ = mass = kg = [M]
r = distance = m = [L]
Therefore,
![[MLT^(-2)] = ([M^(-1)L^(3)T^(-2)][M][M])/([L]^2)\\\\\ [MLT^(-2)] = [M^((-1+1+1))L^((3-2))T^(-2)]\\\\](https://img.qammunity.org/2022/formulas/physics/college/vu1wzewc4moaxld6b5vxc0t9djs4lkizjo.png)
[MLT⁻²] = [MLT⁻²]
Hence, the equation is proven to be homogenous.