Real numbers can be expressed using the following interval,
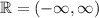
Of course infinities are not just normal infinities but thats out of the scope of this question.
Real numbers less than two can be expressed with,
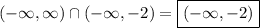
The
 is called intersection ie. where are both intervals valid. First we took real numbers then we intersected them with real numbers valued less than -2 and we got real numbers which are less than -2.
is called intersection ie. where are both intervals valid. First we took real numbers then we intersected them with real numbers valued less than -2 and we got real numbers which are less than -2.
Similarly we can perform with "greater than or equal to 3" real numbers,
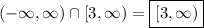
So we have one interval stretching from negative infinity to (but not including) -2, and another interval stretching from including 3 to positive infinity.
If we want numbers in both intervals we can express this two ways,
First way is to use
 union operator to denote we want numbers from two intervals,
union operator to denote we want numbers from two intervals,
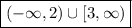
The second way is to specify which numbers we do not want, we do not want -2 and everything up to but not including 3, which is expressed with the following interval
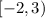
Now we just take out the not wanted interval from real numbers and we will remain with all wanted numbers,
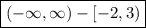
Hope this helps.