Question

The speed of sound where a tuning fork of frequency 262 Hz produces the third resonance position above a closed air column that is 1.59 m in length is ___m/s.

Answer 1

The speed of sound is 555.44 m/s.

Step-by-step explanation:

frequency of third resonance position, f''' = 262 Hz

length of pipe, L = 1.59 m (closed)

Let the speed is v.

The frequency of third resonance in closed organ pipe is

`f''' =(3 v)/(4 L)\\\\262 = (3 v)/(4* 1.59)\\\\v = 555.44 m/s`

Answer 2

v = 333.26 m/s

Step-by-step explanation:

Given that,

The frequency of the tuning fork, f = 262 Hz

It produces the third resonance position above a closed air column that is 1.59 m in length.

We need to find the speed of sound in tuning fork. Let it is f. The third resonance position corresponds to the fifth harmonic of the closed air column. The wavelength in third resonance is given by :

`\lambda=(4)/(5)L\\\\=(4)/(5)* 1.59\\\\=1.272\ m`

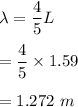
The speed of sound is :

`v=f\lambda\\\\=262* 1.272\\\\=333.26\ m/s`

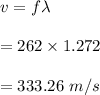
So, the speed of sound is 333.26 m/s.