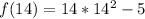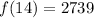Question

Given the equation y=14x2−5, the minimum is ___ and the range is ___

and when x=-14, then f(x)= ____

Answer 1

The minimum is -5

The range is
`y \ge -5`

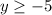
f(14) = 2739

Explanation:

Given

`y = 14x^2 - 5`

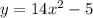
Solving (a): The minimum

A quadratic function is represented as:

`y = ax^2 + bx + c`

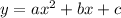
If a > 0, then the function has a minimum

By comparison

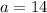`a = 14` --- the function has a minimum

`b = 0`

`c = -5`

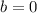
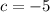
To calculate the minimum, we first calculate the following is calculated as:

`m = -(b)/(2a)`

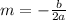
So, we have:

`m = -(0)/(2*14)`

`m = 0`

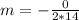
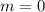
So, the minimum is at f(m)

We have:
`y = 14x^2 - 5`

`f(0) = 14 *0^2 - 5`

`f(0) = - 5`

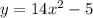
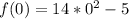
Solving (b): The range

In (a), we have:

`f(0) = - 5` --- the minimum

This implies that the smallest value of y on the graph is -5.

So, the range is:

`r = \y\ge -5\`

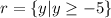
Solving (c): f(14)

We have:

`y = 14x^2 - 5`

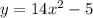
So:

`f(14) = 14 * 14^2 - 5`

`f(14) = 2739`