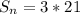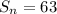Answer:
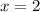
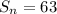
Explanation:
Given
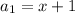
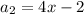
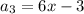
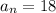
Solving (a): x
To do this, we make use of common difference (d)
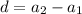
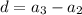
So, we have:
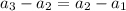
Substitute known values
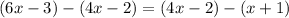
Remove brackets
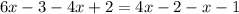
Collect like terms

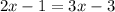
Collect like terms
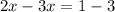
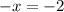
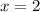
Solving (b): Sum of progression
First, we calculate the first term
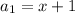
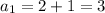
Next, calculate d
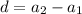
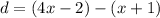
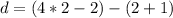

Next, we calculate n using:

Where:
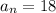
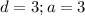
So:
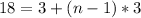
Subtract 3 from both sides
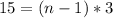
Divide both sides by 3
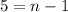
Add 1 to both sides
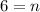

The sum of the progression is:
![S_n = (n)/(2) * [a + a_n]](https://img.qammunity.org/2022/formulas/mathematics/college/bivsg96kkou7dqbvge12efxgm6wbe0bfvf.png)
So,, we have:
![S_n = (6)/(2) * [3 + 18]](https://img.qammunity.org/2022/formulas/mathematics/college/7lcfauqykiw5u0ujpteke3nt0dlapi2m6z.png)