Answer:
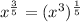
![x^(3)/(5) = \sqrt[5]{x^3}](https://img.qammunity.org/2022/formulas/mathematics/college/85khorkw84o4louggmvxgnevxacvqww2ac.png)
![x^(3)/(5) = (\sqrt[5]{x})^3](https://img.qammunity.org/2022/formulas/mathematics/college/y1rv02ew4fbaehw54k4xb6t84pn83zc1tz.png)
Explanation:
Given
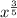
Required
The equivalent expressions
We have:
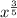
Expand the exponent
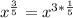
So, we have:
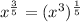 ----- this is equivalent
----- this is equivalent
Express 1/5 as roots (law of indices)
![x^(3)/(5) = \sqrt[5]{x^3}](https://img.qammunity.org/2022/formulas/mathematics/college/85khorkw84o4louggmvxgnevxacvqww2ac.png) ------ this is equivalent
------ this is equivalent
The above can be rewritten as:
![x^(3)/(5) = (\sqrt[5]{x})^3](https://img.qammunity.org/2022/formulas/mathematics/college/y1rv02ew4fbaehw54k4xb6t84pn83zc1tz.png) ------ this is equivalent
------ this is equivalent