Answer:
a) P(0) = 80
b)
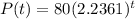
c) 22,363 cells.
d) The rate of growth after 7 hours is of 18,000 bacteria per hour.
e) 9.7 hours.
Explanation:
A bacteria culture grows with a constant relative growth rate.
This means that the population is given by:
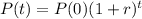
In which P(0) is the initial population and r is the growth rate, as a decimal.
After 2 hours there are 400 bacteria and after 8 hours the count is 50,000.
This means that in 6 hours, the population went from 400 bacteria to 50,000 bacteria. We use this to find r. So
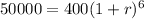
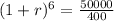
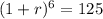
![\sqrt[6]{(1+r)^6} = \sqrt[6]{125}](https://img.qammunity.org/2022/formulas/mathematics/college/i91ex0n76o002xbptk8uyq2hvujjp4umjg.png)
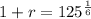
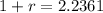
So

(a) Find the initial population. P(0)
We have that P(2) = 400. We use this to find P(0). So

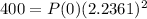
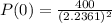
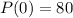
So
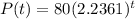
(b) Find an expression for the population after t hours.
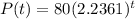
(c) Find the number of cells after 7 hours.
This is P(7). So
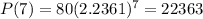
22,363 cells.
(d) Find the rate of growth after 7 hours.
We have to find the derivative when t = 7. So
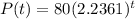
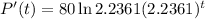
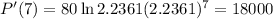
The rate of growth after 7 hours is of 18,000 bacteria per hour.
(e) When will the population reach 200,000?
This is t for which
 . So
. So
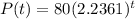
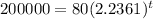
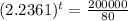
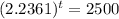
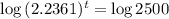
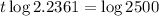
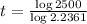
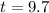
So 9.7 hours.