Answer:
the largest areas that the field could be is
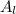 =7587.75 m
=7587.75 m
the smallest areas that the field could be is
 =6318.25 m
=6318.25 m
Step-by-step explanation:
to the find the largest and the smallest area of the field measurement error is to be considered.
we have to find the greatest possible error, since the measurement was made nearest whole mile, the greatest possible error is half of 1 mile and that is 0.5m.
therefore to find the largest possible area we add the error in the mix of the formular for finding the perimeter with the largest width as shown below:
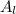 = (L+0.5)(W+0.5)
= (L+0.5)(W+0.5)
(100+0.5)(75+0.5) = (100.5)(75.5) = 7587.75 m
To find the smallest length we will have to subtract instead of adding the error factor value of 0.5 as shown below:
 = (L-0.5)(W-0.5)
= (L-0.5)(W-0.5)
(100-0.5)(64-0.5) = (99.5)(63.5) = 6318.25 m