Answer: Choice D
0 = 16t^2 + 135t + 76; 9 s
==============================================
Step-by-step explanation:
The equation we start with is
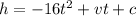
where v is the starting or initial velocity, and c is the starting height.
We're told that v = 135 and c = 76
We let h = 0 to indicate when the object hits the ground, aka the height is 0 ft.
That means the equation updates to
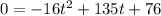
Based on that alone, the answer is between A or D
-------------------
We'll use the quadratic formula to solve for t
We have
So,

We ignore the negative t value because a negative time duration makes no sense.
The only practical solution here is roughly 8.96721 which rounds to 9.0 or simply 9 when we round to the nearest tenth (one decimal place).
In short, the object will hit the ground at the 9 second mark roughly. Or put another way: the object is in the air for about 9 seconds.
From this, we can see that the final answer is choice D.
Keep in mind that we aren't accounting for any wind resistance. Considering this variable greatly complicates the problem and requires much higher level mathematics. So we just assume that there is no wind at this moment.