Answer:
T = 712.9 N
Step-by-step explanation:
First, we will find the speed of the wave:
v = fλ
where,
v = speed of the wave = ?
f = frequency = 890 Hz
λ = wavelength = 0.1 m
Therefore,
v = (890 Hz)(0.1 m)
v = 89 m/s
Now, we will find the linear mass density of the wire:
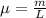
where,
μ = linear mass density of wie = ?
m = mass of wire = 90 g = 0.09 kg
L = length of wire = 1 m
Therefore,
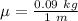
μ = 0.09 kg/m
Now, the tension in wire (T) will be:
T = μv² = (0.09 kg/m)(89 m/s)²
T = 712.9 N