Question

A chemist dissolves 14.0 g of calcium hydroxide in one beaker of water, and 17.0 g of iron(III) chloride

in a second beaker of water. Everything dissolves.
When the two solutions are poured together, solid iron(III) hydroxide precipitates.
1. Write a balanced molecular equation.
2. Determine the identity of the limiting reactant.
3. Predict the mass of iron(III) hydroxide product.

Answer 1

See detailed explanation.

Step-by-step explanation:

Hello there!

In this case, for the given scenario, we will proceed as follows:

1. Here, we infer that the products are iron (III) hydroxide (precipitate) and calcium chloride:

`3Ca(OH)_2+2FeCl_3\rightarrow 3CaCl_2+2Fe(OH)_3`

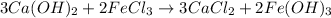
2. In this step we firstly calculate the moles of both reactants, by using their molar masses 74.093 and 162.2 g/mol respectively:

`14.0gCa(OH)_2*(1molCa(OH)_2)/(74.093gCa(OH)_2)=0.189molCa(OH)_2 \\\\17.0gFeCl_3*(1molFeCl_3)/(162.2gFeCl_3)=0.105molFeCl_3`

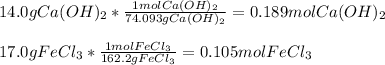
Now, we calculate the moles of calcium hydroxide consumed by 0.105 moles of iron (III) chloride by using the 3:2 mole ratio between them:

`0.105molFeCl_3*(3molCa(OH)_2)/(2molFeCl_3) =0.157molCa(OH)_2`

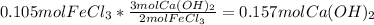
Thus, we infer that calcium hydroxide is in excess as 0.189 moles are available for it but just 0.157 moles react and therefore, iron (III) chloride is the limiting reactant.

3. Here, we use the moles of iron (III) chloride we've just computed, the 2:2 mole ratio with iron (III) hydroxide and its molar mass (106.867 g/mol) as shown below:

`0.105molFeCl_3*(2molFe(OH)_3)/(2molFeCl_3) *(106.867gFe(OH)_3)/(1molFe(OH)_3) \\\\=11.2gFe(OH)_3`

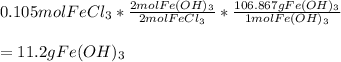
Regards!