Question

A certain drug is used to treat asthma. In a clinical trial of theâ drug, 17 of 258 treated subjects experienced headachesâ (based on data from theâ manufacturer). The accompanying calculator display shows results from a test of the claim that less than 11â% of treated subjects experienced headaches. Use the normal distribution as an approximation to the binomial distribution and assume a 0.01 significance level to complete partsâ (a) throughâ (e) below. â

1-PropZTest
prop<0.11
z=â2.264337000
p=0.0117766978
p=0.0658914729
n=258
a. Is the testâ two-tailed, left-tailed, orâ right-tailed?
b. What is the best statistics?
c. What is the P-value?
d. What is the nut hypothesis and what do you conclude who det hypothesis?
Identify the null hypothesis.
A. H0: pâ 0.11.
B. H0: p=0.11.
C. H0: p<0.11.
D. H0: p>0.11.
Decide whether to reject the null hypothesis.
A. Reject the null hypothesis because theâ P-value is greater than α.
B. Fail to reject the null hypothesis because theâ P-value is less than or equal to α.
C. Reject the null hypothesis because theâ P-value is less than or equal to α.
D. Fail to reject the null hypothesis because theâ P-value is greater than α
e. What is the finalâ conclusion?
A. There is not sufficient evidence to warrant rejection of the claim that less than 11â% of treated subjects experienced headaches.
B. There is not sufficient evidence to support the claim that less than 11â% of treated subjects experienced headaches.
C. There is sufficient evidence to support the claim that less than 11â% of treated subjects experienced headaches.
D. There is sufficient evidence to warrant rejection of the claim that less than 11â% of treated subjects experienced headaches.

Answer 1

a). The test is a left tailed test.

b). The sample proportion is :

`$\hat p = (x)/(n)$`

`$\hat p = (17)/(258)$`

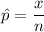
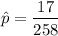
= 0.065

Determining the Z statistics using the formula :

`$Z=\frac{\hat p - p}{\sqrt{(p(1-p))/(n)}}$`

`$Z=\frac{0.065 - 0.11}{\sqrt{(0.11(1-0.11))/(258)}}$`

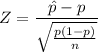
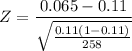
= -2.31

∴ Z statistics value is -2.31

c). Using the excel function, the P-value is :

P-value = Normsdist(-2.31)

= 0.0104441

d). The null hypothesis is
`$H_0: P = 0.11$`

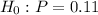
The level of significance is 0.01

We fail to reject the null hypothesis as the P value is less than or equal to the significant level.