Answer:
the probability that a truck drives less than 159 miles in a day = 0.9374
Explanation:
Given;
mean of the truck's speed, (m) = 120 miles per day
standard deviation, d = 23 miles per day
If the mileage per day is normally distributed, we use the following conceptual method to determine the probability of less than 159 miles per day;
1 standard deviation above the mean = m + d, = 120 + 23 = 143
2 standard deviation above the mean = m + 2d, = 120 + 46 = 166
159 is below 2 standard deviation above the mean but greater than 1 standard deviation above the mean.
For normal districution, 1 standard deviation above the mean = 84 percentile
Also, 2 standard deviation above the mean = 98 percentile
143 --------> 84%
159 ---------> x
166 --------- 98%
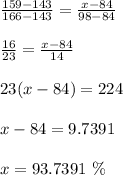
Therefore, the probability that a truck drives less than 159 miles in a day = 0.9374