Question

A series LR circuit contains an emf source of having no internal resistance, a resistor, a inductor having no appreciable resistance, and a switch. If the emf across the inductor is of its maximum value after the switch is closed, what is the resistance of the resistor

Answer 1

b. 1.9 Ω

Step-by-step explanation:

Here is the complete question

A series LR circuit contains an emf source of 14 V having no internal resistance, a resistor, a 34 H inductor having no appreciable resistance, and a switch. If the emf across the inductor is 80% of its maximum value 4.0 s after the switch is closed, what is the resistance of the resistor? a. 1.5 ? b. 1.9 ? c. 5.0 ? d. 14 ?

Solution

The voltage across the inductor V is

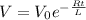`V = V_(0)e^{-(Rt)/(L) }` where V₀ = emf of source = 14 V, R = resistance, L = inductance = 34 H and t = time

Given that V = 80% of its maximum value after 4.0 s, this implies that V = 80 % of V₀ = 0.8V₀ and t = 4.0 s

Since
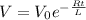`V = V_(0)e^{-(Rt)/(L) }` and V = 0.8V₀.

Since we need to find R, we make R subject of the formula, we have

`V = V_(0)e^{-(Rt)/(L) }`

`V/V_(0)= e^{-(Rt)/(L) }`

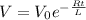
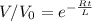
taking natural logarithm of both sides, we have

㏑(V/V₀) = -Rt/L

R = -L㏑(V/V₀)/t

Substituting the values of the variables into the equation, we have

R = -34㏑(0.8V₀/V₀)/4.0 s

R = -34㏑(0.8)/4.0 s

R = -34 × -0.2231/4.0 s

R = 7.587/4

R = 1.896 Ω

R ≅ 1.9 Ω

So, B is the answer